Weismann

LU分解解线性方程组实现

LU分解解线性方程组实现

这里不涉及证明

编程语言使用javascript

先给定一个目标

OJ题目：已知n元线性方程组，2<=n<=50，10000<=各系数<=10000，求解该线性方程组，设定该方程组一定有唯一解。

LU分解法

首先找个题目，题目如下：

3*x1-x2+2*x3=12

x1+2*x2+3*x3=11

2*x1-2*x2-x3=2

LU分解则是将n阶非奇异矩阵转换成两个简单矩阵，这里L是下三角矩阵，U是上三角矩阵，如表格所示

3	-1	2		1	0	0		U11	U12	U13
1	2	3	=	L21	1	0	*	0	U22	U23
2	-2	-1		L31	L32	1		0	0	U33

依次根据左值从左到右，从上到下得出右值未知数结果：

U11=3/1=3

U12=-1/1=-1

U13=2/1=2

L21=1/U11=1/3

U22=(2-L21*U12)/1=7/3

U23=(3-U13*L21)/1=7/3

…

但这仅仅是人的思维，如果以计算机的思路，只能用浮点数计算并且为了套用循环方便，所以计算顺序和结果如下表所示

3	-1	2		3	-1	2		3	-1	2
1	2	3	=>	L21	U22	U23	=>	0.333333	U22	U23	=>	…
2	-2	-1		L31	L32	U33		0.666666	L32	U33

以上我们把LU存到一个二维数组中，初始值为最左边的矩阵，之后为了看着方便，则标记为Lxx、Uxx，变为真实值的则采用原地处理的方式覆盖原值，由此我们总结出公式。

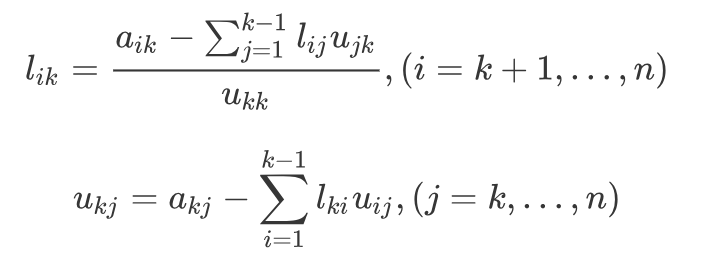
通过以上计算公式，可总结以下算法代码：

for (var k = 0; k < n - 1; k++) {  //进行n-1次循环，因第一行和最后一列不需要计算
    for (var i = k + 1; i < n; i++) {  //L
        for (var j = 0; j < k; j++) {
            data[i][k] -= data[j][k] * data[i][j];
        }
        data[i][k] /= data[k][k];
    }
    for (var j = k + 1; j < n; j++) {  //U
        for (var i = 0; i < k + 1; i++) {
            data[k + 1][j] -= data[k + 1][i] * data[i][j];
        }
    }
}

接下来是回代，由新LU矩阵得出y和x，有以下公式，此处bi是线性方程组矩阵最后一列的值。

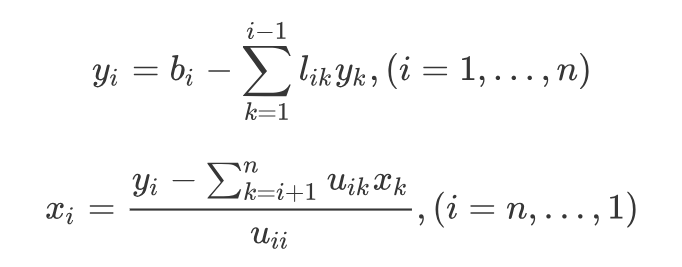
开始进行回代（以下为手算），为了计算方便，我们把LU结果列在下方

LU矩阵

3	-1	2
1/3	7/3	7/3
2/3	-4/7	-1

回代过程

y1=b1=12	x1=(y1-u12x2-u13x3)/u11=3
y2=b2-y1*l21=7	x2=(y2-u23*x3)/u22=1
y3=b3-y2l32-y1l31=-2	x3=y3/u33=2

以上计算过程根据公式总结出算法代码：

  for(var i=0;i<n;i++) {  //yi回代
    var temp=data[i][n];
    for(var j=0;j<=i-1;j++) {
      temp-=data[i][j]*data[j][n];
    }
    data[i][n]=temp;
  }

  for(var i=n-1;i>=0;i--) {  //xi回代
    var temp=data[i][n];
    for(var j=n-1;j>i;j--) {
      temp-=data[i][j]*data[j][n];
    }
    data[i][n]=temp/data[i][i];
  }

结果会因为语言不同造成的浮点数实现不同，从而结果有一丝偏差。

你以为这就完了？不，还有一些情况没有考虑，这里的例子只是最佳情况。

特殊状况

看一下这种情况，题目如下：

2*x2=2

x1=3

如将此方程组作为参数传入以上代码中，则会造成错误，即分母为0的情况。

这时我们引入选主元的的概念。

根据定理，设n*n矩阵非奇异，若对矩阵实施高斯消去过程时主元data[k][k]=0，则该列下方至少有一个元素不为0，即存在ik>k，data[ik][k]!=0。

至此，我们则需要对代码做一些调整，即要保证data[k][k]!=0，所以在分解LU矩阵时修改代码如下：

for (var k = 0; k < n - 1; k++) {  //进行n-1次循环，因第一行和最后一列不需要计算
  if(data[k][k]===0) {  //修改部分
    var temp=[];
    for(var i=k+1;i<n;i++) {
      if(Math.abs(data[i][k])>data[k][k]) {
        [data[k],data[i]]=[data[i],data[k]];
      }
    }
  }
  for (var i = k + 1; i < n; i++) {  //L
    for (var j = 0; j < k; j++) {
      data[i][k] -= data[j][k] * data[i][j];
    }
    data[i][k] /= data[k][k];
  }
  for (var j = k + 1; j < n; j++) {  //U
    for (var i = 0; i < k + 1; i++) {
      data[k + 1][j] -= data[k + 1][i] * data[i][j];
    }
  }
}

完整代码

function a(n,data) {
  for (var k = 0; k < n - 1; k++) {  //进行n-1次循环，因第一行和最后一列不需要计算
    if(data[k][k]===0) {  //选主元
      var temp=[];
      for(var i=k+1;i<n;i++) {
        if(Math.abs(data[i][k])>data[k][k]) {
          [data[k],data[i]]=[data[i],data[k]];
        }
      }
    }
    for (var i = k + 1; i < n; i++) {  //L
      for (var j = 0; j < k; j++) {
        data[i][k] -= data[j][k] * data[i][j];
      }
      data[i][k] /= data[k][k];
    }
    for (var j = k + 1; j < n; j++) {  //U
      for (var i = 0; i < k + 1; i++) {
        data[k + 1][j] -= data[k + 1][i] * data[i][j];
      }
    }
  }

  for (var i = 0; i < n; i++) {  //yi回代
    var temp = data[i][n];
    for (var j = 0; j <= i - 1; j++) {
      temp -= data[i][j] * data[j][n];
    }
    data[i][n] = temp;
  }

  for (var i = n - 1; i >= 0; i--) {  //xi回代
    var temp = data[i][n];
    for (var j = n - 1; j > i; j--) {
      temp -= data[i][j] * data[j][n];
    }
    data[i][n] = temp / data[i][i];
  }

  return data;
}